Earth Speed - How Fast Does the Earth Spin
Did you know that people on the Equator move faster than speed of sound? Check on the map, how fast you are. See, how fast does the Earth rotate on its axis at a given latitude. See, how to calculate rotational speed of the Earth. How fast does the Earth move around the Sun. Sidereal day vs solar day. What is the shape of the Earth? Earth's shape equation.What's on this page
Check "Your Speed" on the Map
Find your speed by clicking the location you are in.
Click on the map to get rotational speed of the Earth at any latitude
"How fast" are the cities?
| City | Lat | km/h | mph | m/s | yd/s |
|---|
How Fast is the Earth rotating at a given latitude
The standard formula for average speed is:
If the Earth is a perfect sphere, simple trigonometry shows us that Rlat = RE*cos(lat).
So, Earth's speed at a given latitude 'lat' will be given by the equation:
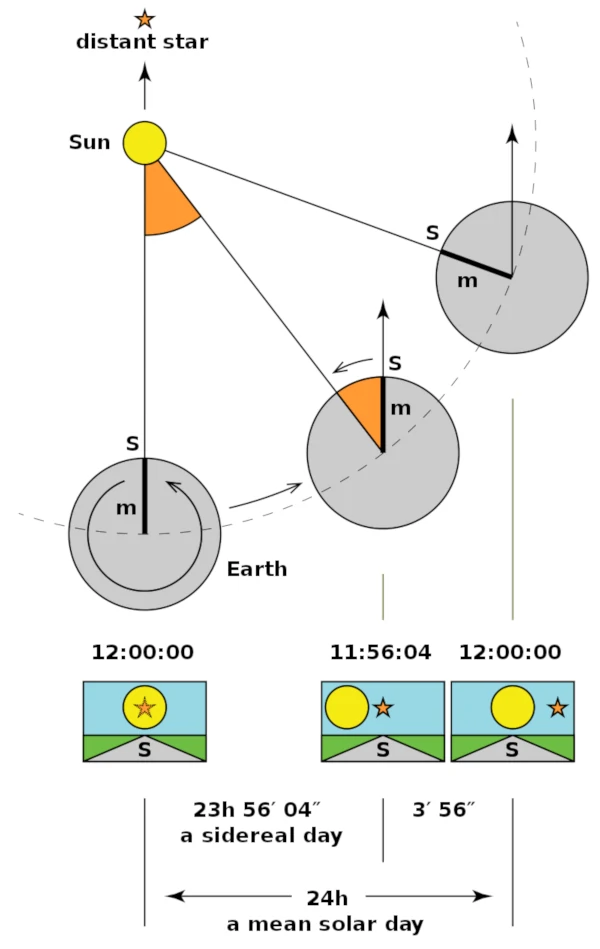Fig 1) Sidereal time vs. solar time. Left (solar time = 12:00:00): a distant star (the small orange star) and the Sun are at culmination, on the local meridian m. Centre (23h 56m 04s later): only the distant star is at culmination (a mean sidereal day). Right (24 hours later, 12:00:00 next day): a few minutes later the Sun is on the local meridian again. A solar day is complete.
Source: Wikipedia, created by: Xaonon, licence: CC BY-SA 4.0
The table below lists the speed of the rotation of the Earth for some latitudes.
Higher-order approximation - bigger font, first approximation - smaller font.
v=s/t
where:- v - average speed
- s - distance traveled
- t - time elapsed
First Approximation (quite good)
Simplifying Assumptions:- The Earth rotates one full turn in 24 hours (t=24 h)
- The Earth is a perfect sphere of radius RE=6,371 km (3958.756 miles)
If the Earth is a perfect sphere, simple trigonometry shows us that Rlat = RE*cos(lat).
So, Earth's speed at a given latitude 'lat' will be given by the equation:
Vlat=2*π*RE*cos(lat)/t = VE*cos(lat)
Higher-order Approximation
In the first approximation two assumptions were made (24 hours day and spherical Earth).
In reality, time for Earth to make one full turn (360 °) on its axis is a little shorter than 24 hours and
the Earth is flattened at the poles and bulges at the Equator - the figure of the Earth is an oblate spheroid or oblate ellipsoid.
Sidereal day vs. Solar day
Everybody knows that Earth's day is 24 hours long, then why we have said that the time to make one full turn is shorter?
Look at the figure 1 - 24 hours (solar day) is the time it takes for the Earth to rotate so that the Sun appears in the same position (left and right Earth on fig 1), but in addition to rotation on its axis, the Earth revolves around the Sun - so, the moment the Earth makes full turn (360 °) is a bit earlier (centre Earth on fig 1). This time - needed for the Earth to make full turn in respect to distant star - is so called 'sidereal day' and is 23 hours, 56 minutes and 4.0905 seconds (23.9344696 hours).
The Shape of the Earth
Due to the centrifugal force created by the Earth’s rotation, our planet is flattened at the poles and bulges at the Equator. The Earth's shape could be approximated with good accuracy by the oblate ellipsoid (ellisoid of revolution).
Thus, the equation of the Earth's shape is:
Sidereal day vs. Solar day
Everybody knows that Earth's day is 24 hours long, then why we have said that the time to make one full turn is shorter?
Look at the figure 1 - 24 hours (solar day) is the time it takes for the Earth to rotate so that the Sun appears in the same position (left and right Earth on fig 1), but in addition to rotation on its axis, the Earth revolves around the Sun - so, the moment the Earth makes full turn (360 °) is a bit earlier (centre Earth on fig 1). This time - needed for the Earth to make full turn in respect to distant star - is so called 'sidereal day' and is 23 hours, 56 minutes and 4.0905 seconds (23.9344696 hours).
The Shape of the Earth
Due to the centrifugal force created by the Earth’s rotation, our planet is flattened at the poles and bulges at the Equator. The Earth's shape could be approximated with good accuracy by the oblate ellipsoid (ellisoid of revolution).
Thus, the equation of the Earth's shape is:
x2/a2+y2/b2+z2/c2=1
where (for the Earth):- a=b=6,378,137.0 meters
- c=6,356,752.3142 meters
Rlat=a*cos(lat)/(1-e2sin2(lat))1/2
where:- e2 (eccentricity) = (a2-c2)/a2 = 0.00669438;
Fig 1) Sidereal time vs. solar time. Left (solar time = 12:00:00): a distant star (the small orange star) and the Sun are at culmination, on the local meridian m. Centre (23h 56m 04s later): only the distant star is at culmination (a mean sidereal day). Right (24 hours later, 12:00:00 next day): a few minutes later the Sun is on the local meridian again. A solar day is complete.
Source: Wikipedia, created by: Xaonon, licence: CC BY-SA 4.0
The table below lists the speed of the rotation of the Earth for some latitudes.
Higher-order approximation - bigger font, first approximation - smaller font.
| Lat | km/h | mph | m/s | yd/s |
|---|
How fast does the Earth travel around the Sun?
The Earth's orbit is an ellipse of the length 940 million km (584 million miles).
One complete orbit takes 1 sidereal year which is 365.256 days (8 766.144 hours).
Thus, the average speed of the Earth traveling the orbit is 940,000,000/8,766.144 = 107,230 km/h (66,620 mph).
